Leet Code 287 Find the Duplicate Number (Medium)

Find the Duplicate Number : Finding a sneaky duplicate number in an array can be a real brain-teaser, especially when you’re told not to mess with the array or use too much memory. But fear not! We’ve got a clever trick up our sleeves to crack this code conundrum.

Understanding the Puzzle:
Imagine this: You're handed an array of integers, and there's a twist. Only one number is repeated, and it's your mission to expose this copycat!

The Algorithm Unveiled:

Behold, the secret sauce lies in a legendary algorithm called “tortoise and hare.” 🐢🐇 Let’s break down this detective code:

Note : tortoise and hare Algorithm Also called Floyd’s Cycle Finding Algorithm

How to get 5✨ on Leet Code with my Own experience

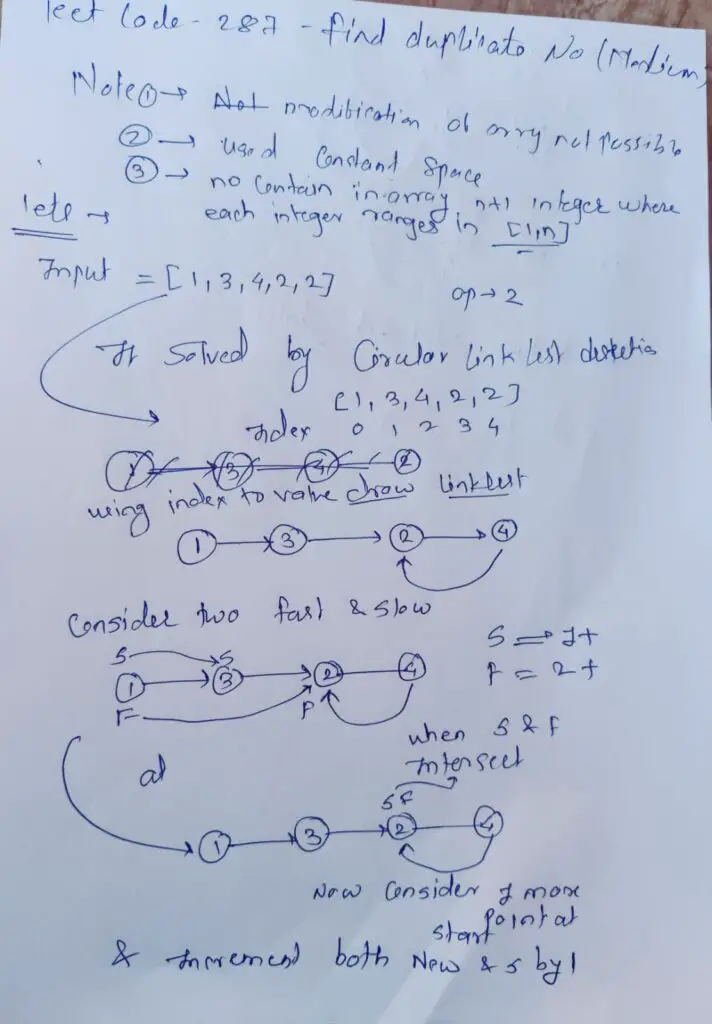
Step 1: The Setup

• Two counting pointers, “slow” and “fast,” start at the same spot – the first element of the array, nums[0]. 🎯

Step 2: Phase 1 – Tracking the Meetup

• In this phase, “slow” moves forward one step, while “fast” moves two steps ahead.
• They keep going until they come to each other like a Hollywood showdown. 💥👊
• What’s the point? This is where the magic begins, and a cycle is born within the array.

Leet Code : Find the Duplicate Number / Element C++ ,Java , Python Solution:

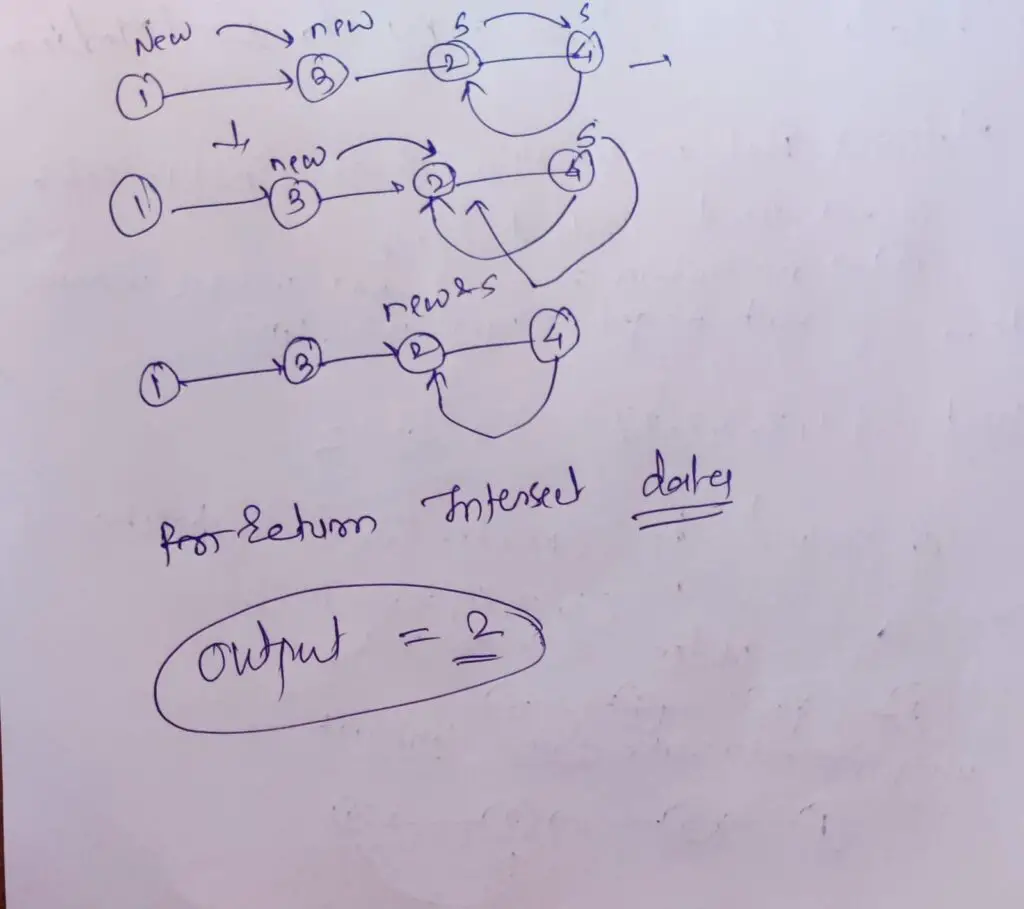
Step 3: Phase 2 – Hare Returns to the Scene

• After finding the epic meetup point, we rewind one of our heroes (either “slow” or “fast”) back to the array’s start, nums[0].
• Now, both pointers move step by step, but guess what? They’ll meet again.
• When they meet together the second time, that’s our jackpot! 🎰 The value they meet at is the elusive duplicated number in the nums array.

Step 4: The Big Reveal

• The secret is out! The number they uncover in Phase 2 is the duplicate you’ve been hunting.
• The best part? The original nums array remains unscathed, and we didn’t gobble up extra memory. 🧠💾

Also Read : Leetcode 135 Candy (Hard) Solution

here’s the code for finding the duplicate number in C++, Python, Java, and JavaScript.

C++:

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int slow = nums[0];
        int fast = nums[0];

        // Phase 1: Find the meeting point
        while (true) {
            slow = nums[slow];
            fast = nums[nums[fast]];
            if (slow == fast) {
                break;
            }
        }

        // Phase 2: Find the start of the cycle
        slow = nums[0];
        while (slow != fast) {
            slow = nums[slow];
            fast = nums[fast];
        }

        return slow;
    }
};

Leet Code :Linked List Cycle II Java || Python || C++ solution

Python:

def findDuplicate(nums):
    slow = nums[0]
    fast = nums[0]

    # Phase 1: Find the meeting point
    while True:
        slow = nums[slow]
        fast = nums[nums[fast]]
        if slow == fast:
            break

    # Phase 2: Find the start of the cycle
    slow = nums[0]
    while slow != fast:
        slow = nums[slow]
        fast = nums[fast]

    return slow

Leet Code : Intersection of Two Linked ListsLeet Code – Java | Python | C++ | Dart | Easy Solution

Java:

public class Solution {
    public int findDuplicate(int[] nums) {
        int slow = nums[0];
        int fast = nums[0];

        // Phase 1: Find the meeting point
        while (true) {
            slow = nums[slow];
            fast = nums[nums[fast]];
            if (slow == fast) {
                break;
            }
        }

        // Phase 2: Find the start of the cycle
        slow = nums[0];
        while (slow != fast) {
            slow = nums[slow];
            fast = nums[fast];
        }

        return slow;
    }
}

JavaScript:

function findDuplicate(nums) {
    let slow = nums[0];
    let fast = nums[0];

    // Phase 1: Find the meeting point
    while (true) {
        slow = nums[slow];
        fast = nums[nums[fast]];
        if (slow === fast) {
            break;
        }
    }

    // Phase 2: Find the start of the cycle
    slow = nums[0];
    while (slow !== fast) {
        slow = nums[slow];
        fast = nums[fast];
    }

    return slow;
}

These code snippets in C++, Python, Java, and JavaScript all implement the same logic for finding the duplicate number using the “tortoise and hare” algorithm.

Leet Code : Three (3) Sum Java | CPP | Python Solution

Conclusion:

By using the “tortoise and hare” trick, we’ve outsmarted the duplicate number puzzle without altering the array or going on a memory . This nifty algorithm showcases the brilliance of problem-solving through clever thinking.

So, next time you’re faced with a similar challenge, remember this elegant solution that keeps the array pristine and memory usage minimal. 🚀🧩

This article decodes the code and its intriguing logic for finding that tricky duplicate number. It showcases the elegance of the “tortoise and hare” algorithm for solving complex puzzles. 🔍🕵️‍♂️